Perplexities regarding the relation between logic and law often stem from the fact that when speaking about ‘logic’, it is not clear enough what it is referred to. Broadly understood, logic is an artificial language providing forms of arguments that preserve truth. In that sense, it is not easy to see a direct relation to law or legal philosophy. However, if logic is related to rationality and reasoning, it seems to underlie activities such as legislation and adjudication, both central concerns of legal theory.
We cannot address the topic of what logic is here (even early analytical philosophers had disagreements about it and so do philosophers of logic nowadays!).
However, what we can – and will – do is focus on two main aspects to which logic has been applied in legal theory:
-
- The reconstruction of legal systems as deductive systems.
- The logical justification of legal decisions.
Although these topics are interrelated, they are conceptually independent. One may, for instance, use logic to reconstruct legal systems deductively without necessarily committing to the view that that the content of judicial decisions are deductive consequences of legal norms.
The reconstruction of legal systems as deductive systems
This first aspect – commonly referred to as the deductive conception of legal systems – involves the assumption that a legal system includes not only the norms explicitly enacted by an authority, but also all the logical consequences derived from them. In its strong version, this view holds that all logical consequences of enacted norms are themselves valid legal norms and, therefore, form part of the system (Alchourrón and Bulygin, 1971). In other words, the legal system can be reconstructed as a set of norms that is closed under logical consequence. In its weaker version, it suggests that the claim that logical consequences “should be taken into account” or that they “are relevant” does not mean that one must accept their membership in each momentary legal system (Navarro and Rodríguez, 2014: 223-229)
Despite this distinction, the core idea is this: logic can be used as a tool to evaluate the completeness and consistency of a system of norms – in other words, to evaluate whether there are normative gaps or contradictions within that system. In this framework, norms are treated as conditional statements: the antecedent represents legally relevant properties, while the consequent indicates the normative solution provided by the authority. The methodology involves selecting the set of legal norms that govern a specific topic (not the whole legal system!) and, by identifying these relevant properties and constructing generic legal cases based on their presence or absence, one can assess whether each generic case has a corresponding legal solution within the system.
The logical justification of judicial decisions
The second aspect concerns the justification of (some types of) legal decisions through what is often called ‘legal syllogism’. Following this, legal reasoning – in particular, judicial reasoning – can be modelled in the likeness of a deductive argument: the first premise is a general legal rule, the second premise is a statement of the relevant facts, and the conclusion – the content of a judicial decision – follows as a deductive consequence via the inference rule called “Modus Ponens”.
This is Modus Ponens:
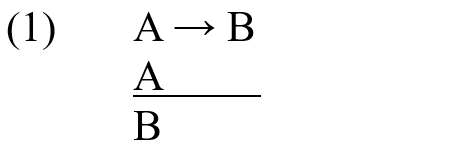
Applying Modus Ponens in law requires adding to the formal vocabulary Deontic Operators to express norms: these are O: Obligatory; Ph: Prohibited; and P: Permitted. It also implies that logic can be used beyond the realm of truth and falsity.
This is the inference rule known as “Deontic Modus Ponens”
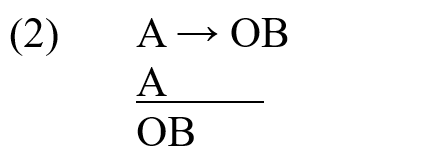
Introducing predicate logic and quantifiers
A deeper logical analysis of judicial reasoning can be provided using the quantificational approach of predicate logic. We need to distinguish, on the one hand, concepts or logical predicates (i.e. what can be said about somebody or something, for example, grammatical constructions with verbs, adjectives or nouns), and, on the other hand, objects or logical individuals (i.e. people, empirical objects, abstract entities, or whatever something can be said about).
This distinction is shown in logical symbolism: capital letters P, Q, R, etc. are used for concepts or logical predicates, and a, b, c, etc. for objects or logical individuals. Logical predicates have an incomplete nature (a sort of empty place is attached to a predicate letter, something like: “P…”), so they must be combined with logical individuals to form an assertion.
Let us take “P” as being “is a horse” and “a” as being “Pegasus”. The formula “Pa” shows the logical structure of the sentence “Pegasus is a horse.”
When something needs to be said not about identified logical individuals, but about all or some individuals of a class, quantifiers are required:
- “∀” (the Universal quantifier) represents the meaning of “all”.
- “∃” (the Existential quantifier) represents the meaning of “some” or similar expressions of natural language.
Quantifiers bound logical variables like x, y, z, and so on. For example, the following formula:
![]()
represents the natural language sentence “All horses are animals”.
Also, the following formula:
![]()
represents natural language sentences such as “Some horses are white” or “There is a horse that is white”.
Now, let us go back to judicial reasoning.
A more complex view of judicial reasoning
Within the new vocabulary of predicate logic, a quantified version of (2) can be constructed. Let us take “H” for “commits homicide”, “S” for “is sanctioned” and “a” for “Mary”. Remember that we are using Deontic Operator “O” to express “Obligatory”.
So, we can write in the logical vocabulary:
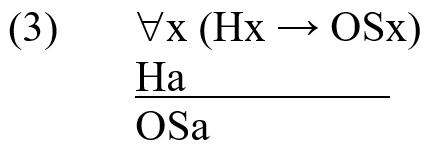
(3) is an example of what is known as ‘legal syllogism’. The first premise expresses: “(All) (or anyone) who commits homicide shall be sanctioned”; here, the Universal quantifier shows the general nature of legal norms. In contrast, the second premise – “Mary committed homicide” – and the conclusion – “It is obligatory that Mary is sanctioned” – show the particular nature of the individual case and that of the judicial decision. The relationship between the first and second premises is commonly referred to as subsumption. This term captures the idea that the second premise constitutes an example, or an instantiation, of the general legal norm expressed in the first premise.
It is important to note that the ‘legal syllogism’ is a schematic reconstruction. Judicial decision-making is a complex process that involves a range of factors, including the identification of norms, interpretation, proof of the facts, evidentiary assessment, and more. The logical reconstruction comes into play only after these various issues have been addressed.
Anyway, the claim that judicial reasoning can be reconstructed as deductive has been criticised. We will see more on this in Part II.
To read more about this, check out this article: Scataglini, M. Gabriela, “Logic in Law: The Positivist School of Buenos Aires”. In: Sellers, M., Kirste, S. (eds) Encyclopedia of the Philosophy of Law and Social Philosophy (2023). https://doi.org/10.1007/978-94-007-6730-0_1109-1
SUGGESTED CITATION: Scataglini, M. Gabriela: “Does logic have any relation to law? (Part I)“, FOLBlog, 2025/7/16, https://fol.ius.bg.ac.rs/2025/07/16/does-logic-have-any-relation-to-law-part-i/


